
Fig. 4 Phase diagram for a binary solid-liquid system
There are many types of different substances that will produce crystals grown from an aqueous solution: sugar and salt for example. Crystals begin to grow when the amount of the substance that is dissolved (the solute) exceeds the amount that in this case the water (the solvent) is capable of dissolving. The maximum amount of solute dissolved in the water produces a solution that is saturated. If additional solute is added, it will not dissolve. By raising the temperature of the water it is possible to dissolve more solute such as sugar in hot coffee than would be possible at lower temperatures. Each substance will have a characteristic solubility that can be experimentally determined. Typical representation of this data is graphical and referred to as a solubility curve.Growing a single crystal such as the NIF-KDP crystal is a very demanding and difficult challenge as the lab photos show. There is a strong tendency for crystals to spontaneously nucleate, i.e., to have many small crystals growing at the same time rather than having a single one grow to a very large size. To be successful in growing a single crystal, the correct regimen must be determined and maintained. Consider the following observations, graphs, diagrams and data. Can you identify the key variables and select appropriate growth conditions to grow a single crystal that has the dimensions of the crystal in the image at the top of the introduction page and in the time that it took to grow the crystal?
Crystal growth from an aqueous solution is based on the existence of metastable regions where spontaneous formation of crystalline nuclei in the solution is impossible, but in this region, it is possible to grow a single crystal from a seed.

Fig. 4 Phase diagram for a binary solid-liquid system
Figure 4 presents a part of a classical phase diagram of a two-component system for a solute with a positive temperature coefficient of solubility dCo/ dT > 0 . The diagram can be described in terms of three zones: (1) the stable zone of unsaturated solution where crystal growth is impossible; (2) the metastable zone where spontaneous crystallization is improbable but crystal growth on a seed occurs, and (3) the labile zone of spontaneous nucleation.Cooling the solution with concentration C from the initial point A´ leads to the point A on the solubility curve. At this point, the solution becomes saturated and can exist in equilibrium with the solid if C =Co(To). Further cooling leads to a state where the concentration of the solute C is higher that the equilibrium concentration Co(T) at a given temperature, and the solution becomes supersaturated. However, spontaneous formation of the solid phase does not occur in this region until a point B on the metastable boundary is reached. If crystallization in a solution saturated at the temperature To starts at the temperature T, the position of the metastable boundary can be expressed in the units of maximum overcooling D T max= To - T, the maximum absolute supersaturation
D Cmax = Co (To) - Co (T),
or in units of relative supersaturation:
s max = D Cmax / Co (T)
One more parameter that characterizes the metastable zone is the induction period ti . It corresponds to the time during which the system can remain without spontaneous nucleation at constant supersaturation within the metastable zone.
 It is possible to grow a single crystal without spontaneous nucleation only within the metastable zone. Additionally, the full period of single crystal growth tg should be less than induction time ti > tg. The practical problem is how to estimate the width of the metastable zone for a particular crystallization system. What should this width be in order to provide for successful growth of a single crystal at high supersaturation during a time that, in the case of large crystals, can exceed one to two months? Experimentation using preselected, constant supersaturation concentrations and constant temperatures provides a guide.
It is possible to grow a single crystal without spontaneous nucleation only within the metastable zone. Additionally, the full period of single crystal growth tg should be less than induction time ti > tg. The practical problem is how to estimate the width of the metastable zone for a particular crystallization system. What should this width be in order to provide for successful growth of a single crystal at high supersaturation during a time that, in the case of large crystals, can exceed one to two months? Experimentation using preselected, constant supersaturation concentrations and constant temperatures provides a guide.Fig. 5. (a) Metastable zone of DKDP solutions. (1) Monoclinic phase solubility; (2) Tetragonal phase solubility; (3) Metastable boundary in the presence of a growing crystal; (4) Metastable boundary without crystals. The region of tetragonal crystals growth is shaded. For comparison the data of Ref. [60] are shown (dotted line). (b) Monoclinic DKDP crystal grown by rapid growth technique at Rz = 16 mm/day. Crystal height is 13 cm.
Fig. 6. Stability of supersaturated KDP solutions: (1) - solubility curve; (2), (3) - metastable boundaries of solutions without (*) and with (n) a growing crystal, respectively; (s) experiments with the empty platform; (4), (5) traditional level of stability from literature data.
Increasing supersaturation is the simplest way to accelerate crystal growth. However, avoiding spontaneous nucleation at high supersaturation is a major challenge that must be overcome.
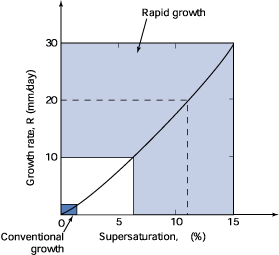
Fig. 7. Approximate comparison of the regions of conventional and rapid growth of KDP crystals (about 40°C). Growth rates can also be increased by increasing the temperature. This means that the higher the temperature, the lower the supersaturation required to obtain the same growth rate.

Fig. 8. Temperature dependencies s(t) corresponding to approximately the constant growth rates of KDP crystals Rz: 10, 20, 30, 40, 50, 60 mm/day. The dashed line is the boundary of the metastable zone.
Actual Data Table
Generally, single crystals can be grown by either a temperature reduction method or using an isothermal method.
The last two parameters to consider are: purity and mass transfer, the latter of which is directly affected by hydrodynamic conditions (e.g.. stirring). The growth rate can be increased by utilizing highly pure raw material, as well as by increasing the velocity of the solution flow relative to the surface of a growing crystal. The increase in growth rate due to chemical purity and hydrodynamic conditions, is generally limited to a factor of two.
| Introduction | Energy/Nuclear Energy | Inertial Confinement Fusion |
| National Ignition Facility/KDP | Solutions & Crystal Growth |