---

There are many definitions for a model. Two of them from Webster's Dictionary are most appropriate to applications in organic chemistry. The first is: "a description or analogy used to help visualize something that cannot be observed". The second is: "a system of postulates, data and inferences presented as a mathematical description of an entity". Molecular Modeling incorporates both definitions.

The background materials in the following links give an idea of the mathematics involved and the basis for computationally generated, energetically minimized images. There are many public domain and commercial software programs that can be used to do this. You have already applied one of these approaches in the WebMO/ Dipole Moment exercise that you completed earlier. The structures in this exercise have been generated and energetically minimized for your use with MacSpartan and stored as .pdb files. You are most welcome and encouraged to continue to use WebMO. You may use WebMO to generate the structures in the exercise and compare the values to those from MacSpartan.

The Schrodinger equation is the basis for quantum mechanics and provides a mathematical model for atomic orbitals. It demands enormous computational power to solve for all but the simplest of atoms and focuses on nuclei, electrons and orbitals. It is virtually impossible to apply it to organic molecules. Several alternatives have evolved which provide approximations through simplification of the classical Schrodinger equation. These alternatives are computational techniques or methods referred to as "Molecular Mechanics" and describe atoms as classical particles whose interactions are represented by potential energy functions based on mechanical force field(s). The simplest model is the sum of all of the energy terms for the structure. An improvement considers various possible conformations for the molecule, and total energy is calculated by considering all of the molecule's possible conformations, summing the energies from individual bond characteristics such as bending, stretching and bond angle, torsional strain and weak repulsive forces. These calculations produce minimized energy structures which are energetically favored conformations for the molecule. A further refinement is Molecular Dynamics which involves additional calculations that include the particle's acceleration and velocity and provide a better correlation to observed data for molecules' physical properties. These approaches offer great possibilities in developing strong visual models for many different large and small molecules. They are widely applied in molecular biology and in bioorganic chemistry particularly for imaging proteins, RNA, DNA as well as small organic molecules.

Molecular orbital theory has produced a wide range of computational methods that perform molecular calculations:

There are also many, many variations within each. See the Computational Chemistry List (CCL) for a list of the hundreds of computational programs that are available.

There are two principal bond features that relate to conformation: (1) There is free rotation about single bonds (sigma bonds), but due to repulsion, spatial distances between atoms are minimized. Therefore, different forms of rotational possibilities will have higher or lower frequency of occurence depending on the proximity and interaction of atoms. (2) Carbon-carbon double bonds have fixed geometry.

Key glossary terms that you are to become familiar with:
rotamer, conformer, syn, gauche, eclipsed, anti, staggered, chair, boat, twist boat, axial, equatorial, cis (Z), trans (E), dihedral angle, inter-atomic distance, torsional strain

See:

1) Dublin City University's: Introduction to Conformational Analysis

2) Western Washington University Virtual Molecular Model Kit

3) University of Illinois, Chicago: Confromational Analysis

Conformational Analysis

Part I:

A) Acyclic conformers: (Butane)

Refer to the following gauche, anti, eclipsed and staggered images of butane and complete the instructions which follow.

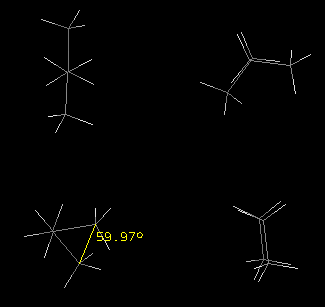
The approximate dihedral angle for conformer number one was determined with a RasMol feature, which is also available with jmol. The angle is relative to the C₁-C₄ carbons and is indicated in yellow. View the four conformational files of butane that are linked below.

1. Draw Newman projection formulas for the four butane conformers:
   
   

   A

   B

   C

   D

   
   
2. Using a viewing perspective through the C₂-C₃ bond, identify each by name.
   
3. Draw a relative, torsional energy diagram starting with a 0^o dihedral angle and rotate about the C₂-C₃ bond through 360^o labeling the conformations of all of the peaks and valleys. Circle the least favored conformer.

B) Conformers in cyclic systems: (Cyclohexane / Ambrox)

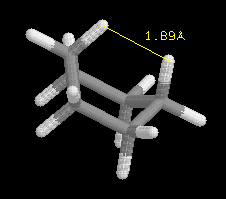
Cyclohexane can exist in a boat or chair conformation. The boat is illustrated below with the interatomic distance in yellow for the "Bowsprit Flagpole" hydrogens to 3 significant figures. Click on the image and change the view of the structure by selecting Render → Scheme → CPK Spacefill → Atoms → 75% vanderWaal's. The image gives an indication of the significant interaction between these two atoms. Their surfaces overlap, which is observed at 100% vanderWaal's. Generally, if the hydrogen atoms are closer than 2.40 Angstroms they will interact "sterically" which is an energetically unfavorable interaction. Steric effects are very important in explaining the conformation and chemical behavior of organic molecules. What is the jmol interatomic distance betweeen the "Bowsprit Flagpole" hydrogens to four significant figures? Is the difference between 3- and 4- "significant"? Briefly explain.

1) Draw line structures for each of the following di-substituted cyclohexane chair forms and label the substitutents as being axial (a) or equatorial. Then draw the chair flipped and label the substituents as being axial (a) or equatorial.

2) Identify each molecule of the following four substituted cyclohexane models as cis- or trans-, and if it is the most energetically stable of the two possible chair forms and why.

A

B

C

D

 

Conformational Analysis

Part II:

Herman Melville describes ambergris in the epoch novel, Moby Dick: ".......ambergris is soft, waxy, and so highly fragrant and spicy, that it is largely used in perfumery, in pastiles, precious candles, hair-powders, and pomatum. The Turks use it in cooking, and also carry it to Mecca, for the same purpose that frankincense is carried to St. Peter's in Rome. Some wine merchants drop a few grains into claret, to flavor it. Who would think, then, that such fine ladies and gentlemen should regale themselves with an essence found in the inglorious bowels of a sick whale! Yet so it is."

Moby Dick or The Whale was written by Melville in 1851. If you are interested in reading the novel, it is available on the Web: http://www.americanliterature.com/MD/MDINDEX.HTML

For further background information on ambergris, ambrox and ambreine see Dr. Randy Ralph's comprehensive site: "Ambergris: A Pathfinder and Annotated Bibliography" http://www.netstrider.com/documents/ambergris

Since the decline of whaling and the restriction of global whaling operations, ambergris has not been commercially used for some time. With the loss of this material, the perfume industry turned to organic synthesis to prepare a substitute, and many, many compounds were synthesized and tested. One that was selected for use is Ambrox. In analyzing the correlation between structure and the smell of the synthesized analogs it was found that certain positions and interatomic distances were critical for the bio-activity. 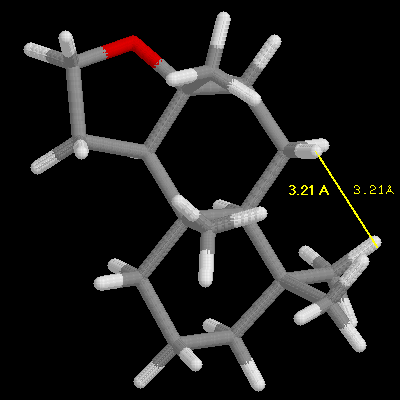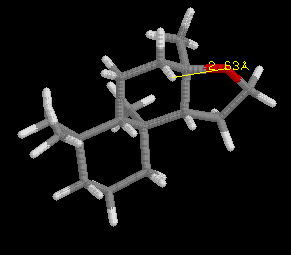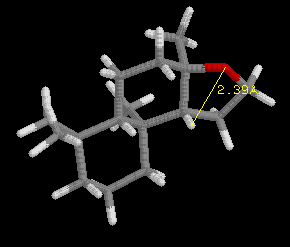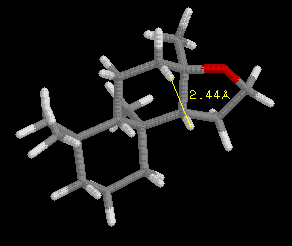This discovery was framed as the "ambergris triangle" which is illustrated by the examples in the following three images, and later became know as the "Triaxial Rule". In order to smell like ambergris the analogs must have two axial hydrogens within 2.38 Angstroms +/-0.35 A of each other, and one hydrogen must be within 2.90 Angstroms +/-0.40 A of an oxygen atom in an adjacent ring, with the other hydrogen 2.45 Angstroms +/-0.35 A from the oxygen atom. Ambrox meets these criteria as illustrated in the examples with RasMol.
 
Define the distances in the spatial triangle for Analog A and Analog B, and determine if one, or the other, or both will smell like ambergris. Be sure to clearly state your conclusion. Note: the ring system is different than Ambrox, but the Rule still applies.